Exploratory Data Analysis (EDA) and Unsupervised Learning
Loading and exploring data
The data that we will be using for this workshop are from the following sources:
- The Breast Cancer Wisconsin (Diagnostic) Data Set from the UCI Machine Learning repository.
- RNA-Seq data from the study of tooth growth in mouse embryos from the Gene Expression Omnibus ID:GSE76316
We will first load up the UCI dataset. The dataset itself does not contain column names, we’ve created a second file with only the column names, which we will use. We will be using tidyverse, a collection of R packages for Data Science.
library(tidyverse) # working with data frames, plotting
breastCancerData <- read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data",
col_names = FALSE)
breastCancerDataColNames <- read_csv("https://raw.githubusercontent.com/fpsom/2021-06-ml-elixir-fr/main/data/wdbc.colnames.csv",
col_names = FALSE)
colnames(breastCancerData) <- breastCancerDataColNames$X1
# Check out head of dataframe
breastCancerData %>% head()
If all goes well, we can see that our dataset contains 569 observations across 32 variables. This is what the first 6 lines look like:
# A tibble: 6 x 32
ID Diagnosis Radius.Mean Texture.Mean Perimeter.Mean Area.Mean Smoothness.Mean
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 8.42e5 M 18.0 10.4 123. 1001 0.118
2 8.43e5 M 20.6 17.8 133. 1326 0.0847
3 8.43e7 M 19.7 21.2 130 1203 0.110
4 8.43e7 M 11.4 20.4 77.6 386. 0.142
5 8.44e7 M 20.3 14.3 135. 1297 0.100
6 8.44e5 M 12.4 15.7 82.6 477. 0.128
# ... with 25 more variables: Compactness.Mean <dbl>, Concavity.Mean <dbl>,
# Concave.Points.Mean <dbl>, Symmetry.Mean <dbl>, Fractal.Dimension.Mean <dbl>,
# Radius.SE <dbl>, Texture.SE <dbl>, Perimeter.SE <dbl>, Area.SE <dbl>,
# Smoothness.SE <dbl>, Compactness.SE <dbl>, Concavity.SE <dbl>, Concave.Points.SE <dbl>,
# Symmetry.SE <dbl>, Fractal.Dimension.SE <dbl>, Radius.Worst <dbl>, Texture.Worst <dbl>,
# Perimeter.Worst <dbl>, Area.Worst <dbl>, Smoothness.Worst <dbl>,
# Compactness.Worst <dbl>, Concavity.Worst <dbl>, Concave.Points.Worst <dbl>,
# Symmetry.Worst <dbl>, Fractal.Dimension.Worst <dbl>
We will also make our Diagnosis column a factor:
Question: What is a factor?
# Make Diagnosis a factor
breastCancerData$Diagnosis <- as.factor(breastCancerData$Diagnosis)
What is Exploratory Data Analysis (EDA) and why is it useful?
Before thinking about modeling, have a look at your data. There is no point in throwing a 10000 layer convolutional neural network (whatever that means) at your data before you even know what you’re dealing with.
We will first remove the first column, which is the unique identifier of each row:
Question: Why?
# Remove first column
breastCancerDataNoID <- breastCancerData[2:ncol(breastCancerData)]
# View head
breastCancerDataNoID %>% head()
The output should like like this:
# A tibble: 6 x 31
Diagnosis Radius.Mean Texture.Mean Perimeter.Mean Area.Mean Smoothness.Mean
<fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 M 18.0 10.4 123. 1001 0.118
2 M 20.6 17.8 133. 1326 0.0847
3 M 19.7 21.2 130 1203 0.110
4 M 11.4 20.4 77.6 386. 0.142
5 M 20.3 14.3 135. 1297 0.100
6 M 12.4 15.7 82.6 477. 0.128
# ... with 25 more variables: Compactness.Mean <dbl>, Concavity.Mean <dbl>,
# Concave.Points.Mean <dbl>, Symmetry.Mean <dbl>, Fractal.Dimension.Mean <dbl>,
# Radius.SE <dbl>, Texture.SE <dbl>, Perimeter.SE <dbl>, Area.SE <dbl>,
# Smoothness.SE <dbl>, Compactness.SE <dbl>, Concavity.SE <dbl>, Concave.Points.SE <dbl>,
# Symmetry.SE <dbl>, Fractal.Dimension.SE <dbl>, Radius.Worst <dbl>, Texture.Worst <dbl>,
# Perimeter.Worst <dbl>, Area.Worst <dbl>, Smoothness.Worst <dbl>,
# Compactness.Worst <dbl>, Concavity.Worst <dbl>, Concave.Points.Worst <dbl>,
# Symmetry.Worst <dbl>, Fractal.Dimension.Worst <dbl>
We have many variables in this dataset. For the interest of time, we will focus only on the first five. Let’s have a look at a plot:
library(GGally)
ggpairs(breastCancerDataNoID[1:5], aes(color=Diagnosis, alpha=0.4))
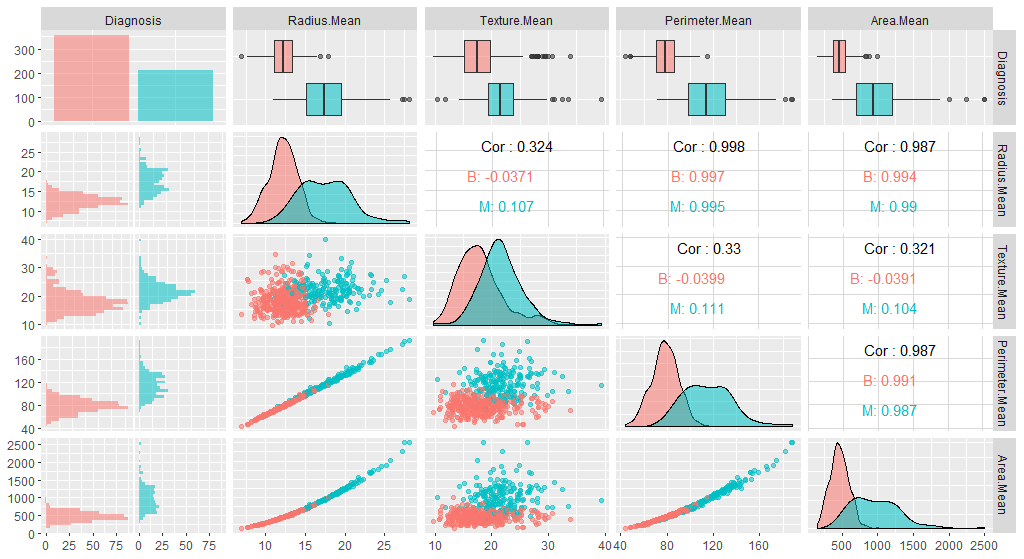
Note that the features have widely varying centers and scales (means and standard deviations), so we’ll want to center and scale them in some situations. We will use the [caret](https://cran.r-project.org/web/packages/caret/vignettes/caret.html) package for this, and specifically, the preProcess function.
The preProcess function can be used for many operations on predictors, including centering and scaling. The function preProcess estimates the required parameters for each operation and predict.preProcess is used to apply them to specific data sets. This function can also be interfaced when calling the train function.
library(caret)
# Center & scale data
ppv <- preProcess(breastCancerDataNoID, method = c("center", "scale"))
breastCancerDataNoID_tr <- predict(ppv, breastCancerDataNoID)
Let’s have a look on the impact of this process by viewing the summary of the first 5 variables before and after the process:
# Summarize first 5 columns of the original data
breastCancerDataNoID[1:5] %>% summary()
The resulting summary should look like this:
Diagnosis Radius.Mean Texture.Mean Perimeter.Mean Area.Mean
B:357 Min. : 6.981 Min. : 9.71 Min. : 43.79 Min. : 143.5
M:212 1st Qu.:11.700 1st Qu.:16.17 1st Qu.: 75.17 1st Qu.: 420.3
Median :13.370 Median :18.84 Median : 86.24 Median : 551.1
Mean :14.127 Mean :19.29 Mean : 91.97 Mean : 654.9
3rd Qu.:15.780 3rd Qu.:21.80 3rd Qu.:104.10 3rd Qu.: 782.7
Max. :28.110 Max. :39.28 Max. :188.50 Max. :2501.0
Let’s check the summary of the re-centered and scaled data
# Summarize first 5 columns of the re-centered and scaled data
breastCancerDataNoID_tr[1:5] %>% summary()
It now should look like this:
Diagnosis Radius.Mean Texture.Mean Perimeter.Mean Area.Mean
B:357 Min. :-2.0279 Min. :-2.2273 Min. :-1.9828 Min. :-1.4532
M:212 1st Qu.:-0.6888 1st Qu.:-0.7253 1st Qu.:-0.6913 1st Qu.:-0.6666
Median :-0.2149 Median :-0.1045 Median :-0.2358 Median :-0.2949
Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
3rd Qu.: 0.4690 3rd Qu.: 0.5837 3rd Qu.: 0.4992 3rd Qu.: 0.3632
Max. : 3.9678 Max. : 4.6478 Max. : 3.9726 Max. : 5.2459
As, we can observe here, all variables in our new data have a mean of 0 while maintaining the same distribution of the values. However, this also means that the absolute values do not correspond to the “real”, original data - and is just a representation of them.
We can also check whether our plot has changed with the new data:
library(GGally)
ggpairs(breastCancerDataNoID_tr[1:5], aes(color=Diagnosis, alpha=0.4))
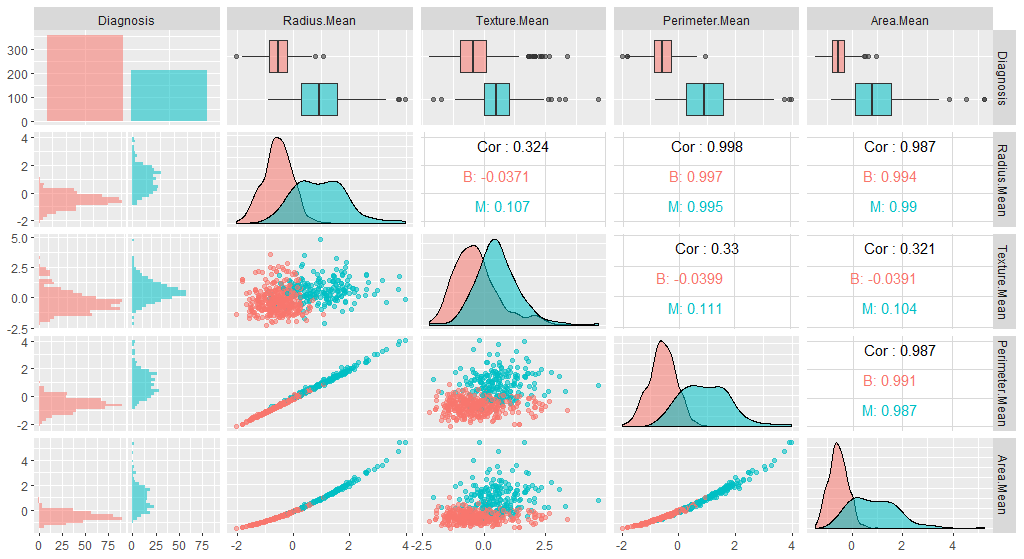
Question: Do you see any differences?
Unsupervised Learning
Dimensionality Reduction and PCA
Machine learning is the science and art of giving computers the ability to learn to make decisions from data without being explicitly programmed.
Unsupervised learning, in essence, is the machine learning task of uncovering hidden patterns and structures from unlabeled data. For example, a researcher might want to group their samples into distinct groups, based on their gene expression data without in advance what these categories maybe. This is known as clustering, one branch of unsupervised learning.
Supervised learning (which will be addressed later in depth), is the branch of machine learning that involves predicting labels, such as whether a tumor will be benign or malignant.
Another form of unsupervised learning, is dimensionality reduction; in the UCI dataset, for example, there are too many features to keep track of. What if we could reduce the number of features yet still keep much of the information?
Principal component analysis (PCA) is one of the most commonly used methods of dimensionality reduction, and extracts the features with the largest variance. What PCA essentially does is the following:
- The first step of PCA is to decorrelate your data and this corresponds to a linear transformation of the vector space your data lie in;
- The second step is the actual dimension reduction; what is really happening is that your decorrelation step (the first step above) transforms the features into new and uncorrelated features; this second step then chooses the features that contain most of the information about the data.
Let’s have a look into the variables that we currently have, and apply PCA to them. As you can see, we will be using only the numerical variables (i.e. we will exclude the first two, ID and Diagnosis):
ppv_pca <- prcomp(breastCancerData[3:ncol(breastCancerData)], center = TRUE, scale. = TRUE)
We can use the summary() function to get a summary of the PCA:
summary(ppv_pca)
The resulting table, shows us the importance of each Principal Component; the standard deviation, the proportion of the variance that it captures, as well as the cumulative proportion of variance capture by the principal components.
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9
Standard deviation 3.6444 2.3857 1.67867 1.40735 1.28403 1.09880 0.82172 0.69037 0.6457
Proportion of Variance 0.4427 0.1897 0.09393 0.06602 0.05496 0.04025 0.02251 0.01589 0.0139
Cumulative Proportion 0.4427 0.6324 0.72636 0.79239 0.84734 0.88759 0.91010 0.92598 0.9399
PC10 PC11 PC12 PC13 PC14 PC15 PC16 PC17
Standard deviation 0.59219 0.5421 0.51104 0.49128 0.39624 0.30681 0.28260 0.24372
Proportion of Variance 0.01169 0.0098 0.00871 0.00805 0.00523 0.00314 0.00266 0.00198
Cumulative Proportion 0.95157 0.9614 0.97007 0.97812 0.98335 0.98649 0.98915 0.99113
PC18 PC19 PC20 PC21 PC22 PC23 PC24 PC25 PC26
Standard deviation 0.22939 0.22244 0.17652 0.1731 0.16565 0.15602 0.1344 0.12442 0.09043
Proportion of Variance 0.00175 0.00165 0.00104 0.0010 0.00091 0.00081 0.0006 0.00052 0.00027
Cumulative Proportion 0.99288 0.99453 0.99557 0.9966 0.99749 0.99830 0.9989 0.99942 0.99969
PC27 PC28 PC29 PC30
Standard deviation 0.08307 0.03987 0.02736 0.01153
Proportion of Variance 0.00023 0.00005 0.00002 0.00000
Cumulative Proportion 0.99992 0.99997 1.00000 1.00000
Principal Components are the underlying structure in the data. They are the directions where there is the most variance, the directions where the data is most spread out. This means that we try to find the straight line that best spreads the data out when it is projected along it. This is the first principal component, the straight line that shows the most substantial variance in the data.
PCA is a type of linear transformation on a given data set that has values for a certain number of variables (coordinates) for a certain amount of spaces. In this way, you transform a set of x correlated variables over y samples to a set of p uncorrelated principal components over the same samples.
Where many variables correlate with one another, they will all contribute strongly to the same principal component. Where your initial variables are strongly correlated with one another, you will be able to approximate most of the complexity in your dataset with just a few principal components. As you add more principal components, you summarize more and more of the original dataset. Adding additional components makes your estimate of the total dataset more accurate, but also more unwieldy.
Every eigenvector has a corresponding eigenvalue. Simply put, an eigenvector is a direction, such as “vertical” or “45 degrees”, while an eigenvalue is a number telling you how much variance there is in the data in that direction. The eigenvector with the highest eigenvalue is, therefore, the first principal component. The number of eigenvalues and eigenvectors that exits is equal to the number of dimensions the data set has. In our case, we had 30 variables (32 original, minus the first two), so we have produced 30 eigenvectors / PCs. And we can see that we can address more than 95% of the variance (0.95157) using only the first 10 PCs.
We should also have a deeper look in our PCA object:
str(ppv_pca)
The output should look like this:
List of 5
$ sdev : num [1:30] 3.64 2.39 1.68 1.41 1.28 ...
$ rotation: num [1:30, 1:30] -0.219 -0.104 -0.228 -0.221 -0.143 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:30] "Radius.Mean" "Texture.Mean" "Perimeter.Mean" "Area.Mean" ...
.. ..$ : chr [1:30] "PC1" "PC2" "PC3" "PC4" ...
$ center : Named num [1:30] 14.1273 19.2896 91.969 654.8891 0.0964 ...
..- attr(*, "names")= chr [1:30] "Radius.Mean" "Texture.Mean" "Perimeter.Mean" "Area.Mean" ...
$ scale : Named num [1:30] 3.524 4.301 24.299 351.9141 0.0141 ...
..- attr(*, "names")= chr [1:30] "Radius.Mean" "Texture.Mean" "Perimeter.Mean" "Area.Mean" ...
$ x : num [1:569, 1:30] -9.18 -2.39 -5.73 -7.12 -3.93 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr [1:30] "PC1" "PC2" "PC3" "PC4" ...
- attr(*, "class")= chr "prcomp"
The information listed captures the following:
- The center point (
$center), scaling ($scale) and the standard deviation($sdev) of each original variable - The relationship (correlation or anticorrelation, etc) between the initial variables and the principal components (
$rotation) - The values of each sample in terms of the principal components (
$x)
Let’s try to visualize the results we’ve got so far. We will be using the ggbiplot library for this purpose.
ggbiplot(ppv_pca, choices=c(1, 2),
labels=rownames(breastCancerData),
ellipse=TRUE,
groups = breastCancerData$Diagnosis,
obs.scale = 1,
var.axes=TRUE, var.scale = 1) +
ggtitle("PCA of Breast Cancer Dataset")+
theme_minimal()+
theme(legend.position = "bottom")
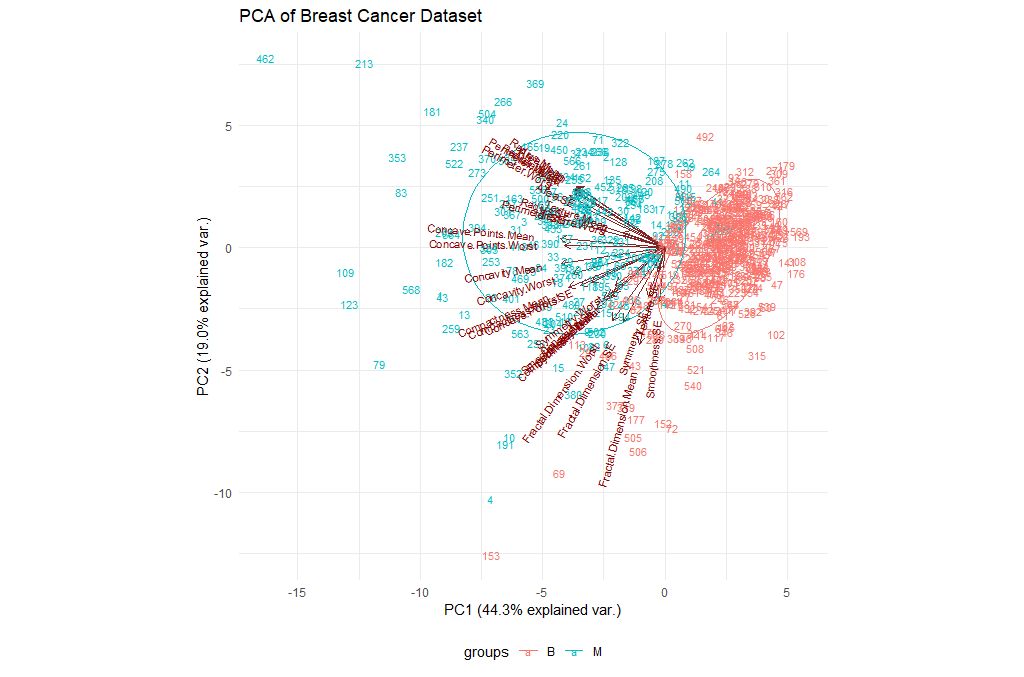
| Exercises | |
|---|---|
| 1 | Try changing the parameters of the plot. For example, check the choices and the var.scale. Is there an impact? What does this mean? |
| 2 | We have been using the entire table of data. What if we restrict our analysis on the mean values (i.e. columns 3-12)? Is there an impact? |
Clustering
One popular technique in unsupervised learning is clustering. As the name itself suggests, Clustering algorithms group a set of data points into subsets or clusters. The algorithms’ goal is to create clusters that are coherent internally, but clearly different from each other externally. In other words, entities within a cluster should be as similar as possible and entities in one cluster should be as dissimilar as possible from entities in another.
Broadly speaking there are two ways of clustering data points based on the algorithmic structure and operation, namely agglomerative and divisive.
- Agglomerative: An agglomerative approach begins with each observation in a distinct (singleton) cluster, and successively merges clusters together until a stopping criterion is satisfied.
- Divisive: A divisive method begins with all patterns in a single cluster and performs splitting until a stopping criterion is met.
Essentially, this is the task of grouping your data points, based on something about them, such as closeness in space. Clustering is more of a tool to help you explore a dataset, and should not always be used as an automatic method to classify data. Hence, you may not always deploy a clustering algorithm for real-world production scenario. They are often too unreliable, and a single clustering alone will not be able to give you all the information you can extract from a dataset.
K-Means
What we are going to do is group the tumor data points into two clusters using an algorithm called k-means, which aims to cluster the data in order to minimize the variances of the clusters. The basic idea behind k-means clustering consists of defining clusters so that the total intra-cluster variation (known as total within-cluster variation) is minimized. There are several k-means algorithms available. However, the standard algorithm defines the total within-cluster variation as the sum of squared distances Euclidean distances between items and the corresponding centroid:
Let’s cluster our data points (ignoring their know classes) using k-means and then we’ll compare the results to the actual labels that we know:
set.seed(1)
km.out <- kmeans(breastCancerData[3:ncol(breastCancerData)], centers=2, nstart=20)
The nstart option attempts multiple initial configurations and reports on the best one within the kmeans function. Seeds allow us to create a starting point for randomly generated numbers, so that each time our code is run, the same answer is generated.
Also, note that k-means requires the number of clusters to be defined beforehand and given via the centers option.
Let’s check now what the output contains:
str(km.out)
The output will be:
List of 9
$ cluster : int [1:569] 2 2 2 1 2 1 2 1 1 1 ...
$ centers : num [1:2, 1:30] 12.6 19.4 18.6 21.7 81.1 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:2] "1" "2"
.. ..$ : chr [1:30] "Radius.Mean" "Texture.Mean" "Perimeter.Mean" "Area.Mean" ...
$ totss : num 2.57e+08
$ withinss : num [1:2] 28559677 49383423
$ tot.withinss: num 77943100
$ betweenss : num 1.79e+08
$ size : int [1:2] 438 131
$ iter : int 1
$ ifault : int 0
- attr(*, "class")= chr "kmeans"
The information contained here is:
$cluster: a vector of integers (from 1:k) indicating the cluster to which each point is allocated.$centers: a matrix of cluster centers.$withinss: vector of within-cluster sum of squares, one component per cluster.$tot.withinss: total within-cluster sum of squares (i.e.sum(withinss)).$size: the number of points in each cluster.
Let’s have a look at the clusters, and we will do this in relationship to the principal components we identified earlier:
ggplot(as.data.frame(ppv_pca$x), aes(x=PC1, y=PC2, color=as.factor(km.out$cluster), shape = breastCancerData$Diagnosis)) +
geom_point( alpha = 0.6, size = 3) +
theme_minimal()+
theme(legend.position = "bottom") +
labs(title = "K-Means clusters against PCA", x = "PC1", y = "PC2", color = "Cluster", shape = "Diagnosis")
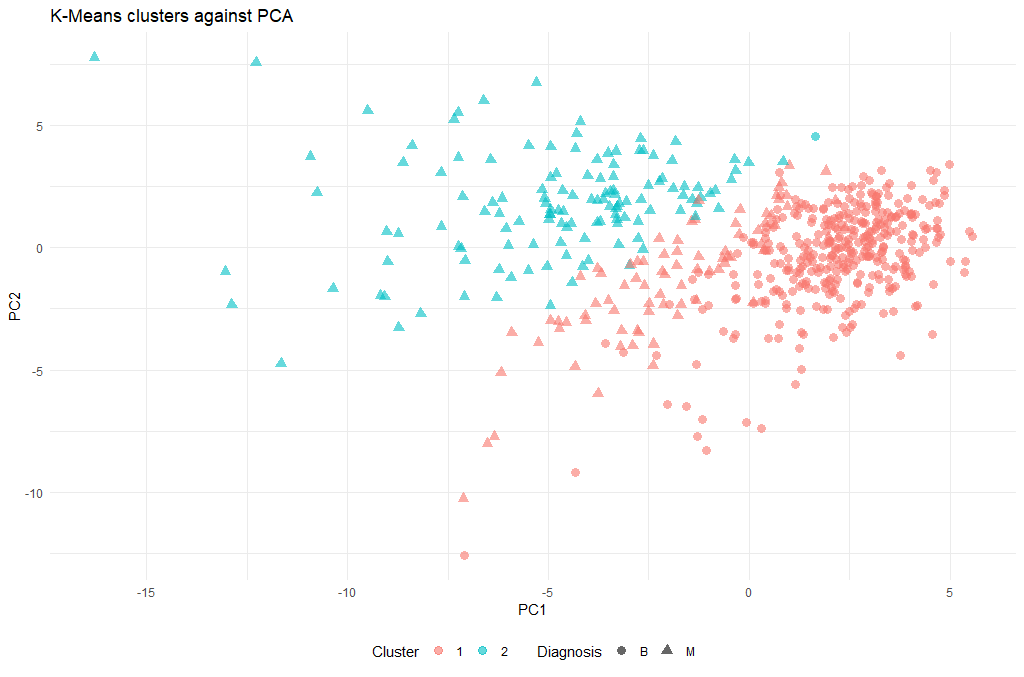
(There is a lot of information to unpack here, so we will discuss during the course what these 5 lines of code actually do)
Now that we have a cluster for each tumor (clusters 1 and 2), we can check how well they coincide with the labels that we know. To do this we will use a cool method called cross-tabulation: a cross-tab is a table that allows you to read off how many data points in clusters 1 and 2 were actually benign or malignant respectively.
# Cross-tab of clustering & known labels
library(gmodels)
CrossTable(breastCancerData$Diagnosis, km.out$cluster)
The output should look like this:
Cell Contents
|-------------------------|
| N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 569
| km.out$cluster
breastCancerData$Diagnosis | 1 | 2 | Row Total |
---------------------------|-----------|-----------|-----------|
B | 356 | 1 | 357 |
| 23.988 | 80.204 | |
| 0.997 | 0.003 | 0.627 |
| 0.813 | 0.008 | |
| 0.626 | 0.002 | |
---------------------------|-----------|-----------|-----------|
M | 82 | 130 | 212 |
| 40.395 | 135.060 | |
| 0.387 | 0.613 | 0.373 |
| 0.187 | 0.992 | |
| 0.144 | 0.228 | |
---------------------------|-----------|-----------|-----------|
Column Total | 438 | 131 | 569 |
| 0.770 | 0.230 | |
---------------------------|-----------|-----------|-----------|
Question: How well did the clustering work?
Optimal k
One technique to choose the best k is called the elbow method. This method uses within-group homogeneity or within-group heterogeneity to evaluate the variability. In other words, you are interested in the percentage of the variance explained by each cluster. You can expect the variability to increase with the number of clusters, alternatively, heterogeneity decreases. Our challenge is to find the k that is beyond the diminishing returns. Adding a new cluster does not improve the variability in the data because very few information is left to explain.
First of all, let’s create a function that computes the total within clusters sum of squares:
kmean_withinss <- function(k) {
cluster <- kmeans(breastCancerData[3:ncol(breastCancerData)], k)
return (cluster$tot.withinss)
}
We can try for a single k (e.g. 2), and see the value:
kmean_withinss(2)
[1] 77943100
However, we need to test this n times. We will use the sapply() function to run the algorithm over a range of k. This technique is faster than creating a loop and store the value each time.
# Set maximum cluster
max_k <-20
# Run algorithm over a range of k
wss <- sapply(2:max_k, kmean_withinss)
Finally, let’s save the results into a data frame, so that we can work with it:
# Create a data frame to plot the graph
elbow <-data.frame(2:max_k, wss)
Now that we have the data, we can plot them and try to identify the “elbow” point:
# Plot the graph with gglop
ggplot(elbow, aes(x = X2.max_k, y = wss)) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = seq(1, 20, by = 1))
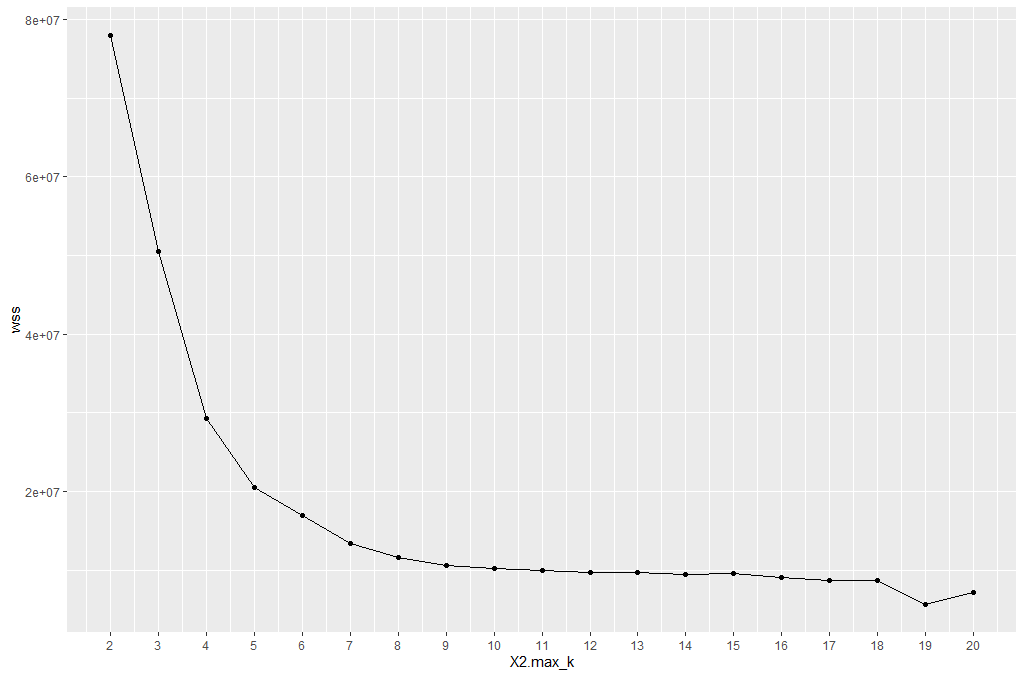
From the graph, you can see the optimal k is around 10, where the curve is starting to have a diminishing return.
| Exercises | |
|---|---|
| 1 | Try re-running the clustering step with the new k. Is there a significant difference? |
| 2 | Try to think of alternative metrics that could be used as a “distance” measure, instead of the default “Euclidean”. Do you think there might be an optimal for our case? |
Hierarchical clustering
k-means clustering requires us to specify the number of clusters, and determining the optimal number of clusters is often not trivial. Hierarchical clustering is an alternative approach which builds a hierarchy from the bottom-up, and doesn’t require us to specify the number of clusters beforehand but requires extra steps to extract final clusters. The algorithm works as follows:
- Put each data point in its own cluster.
- Identify the closest two clusters and combine them into one cluster.
- Repeat the above step till all the data points are in a single cluster.
Once this is done, it is usually represented by a dendrogram like structure. There are a few ways to determine how close two clusters are:
- Complete linkage clustering: Find the maximum possible distance between points belonging to two different clusters.
- Single linkage clustering: Find the minimum possible distance between points belonging to two different clusters.
- Mean linkage clustering: Find all possible pairwise distances for points belonging to two different clusters and then calculate the average.
- Centroid linkage clustering: Find the centroid of each cluster and calculate the distance between centroids of two clusters.
We will be applying Hierarchical clustering to our dataset, and see what the result might be. Remember that our dataset has some columns with nominal (categorical) values (columns ID and Diagnosis), so we will need to make sure we only use the columns with numerical values. There are no missing values in this dataset that we need to clean before clustering. But the scales of the features are different and we need to normalize it.
breastCancerDataScaled <- as.data.frame(scale(breastCancerData[3:ncol(breastCancerData)]))
summary(breastCancerDataScaled)
We can now proceed with creating the distance matrix:
dist_mat <- dist(breastCancerDataScaled, method = 'euclidean')
There are several options for method: euclidean, maximum, manhattan, canberra, binary or minkowski.
The next step is to actually perform the hierarchical clustering, which means that at this point we should decide which linkage method we want to use. We can try all kinds of linkage methods and later decide on which one performed better. Here we will proceed with average linkage method (i.e. UPGMA); other methods include ward.D, ward.D2, single, complete, mcquitty (= WPGMA), median (= WPGMC) and centroid (= UPGMC).
hclust_avg <- hclust(dist_mat, method = 'average')
plot(hclust_avg)
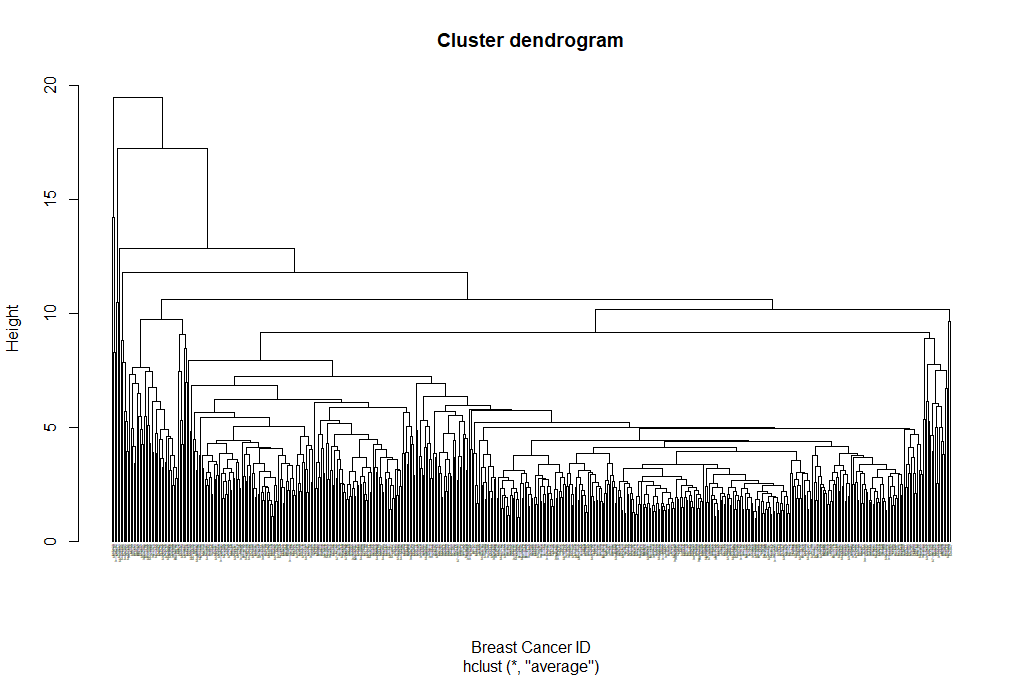
Notice how the dendrogram is built and every data point finally merges into a single cluster with the height(distance) shown on the y-axis.
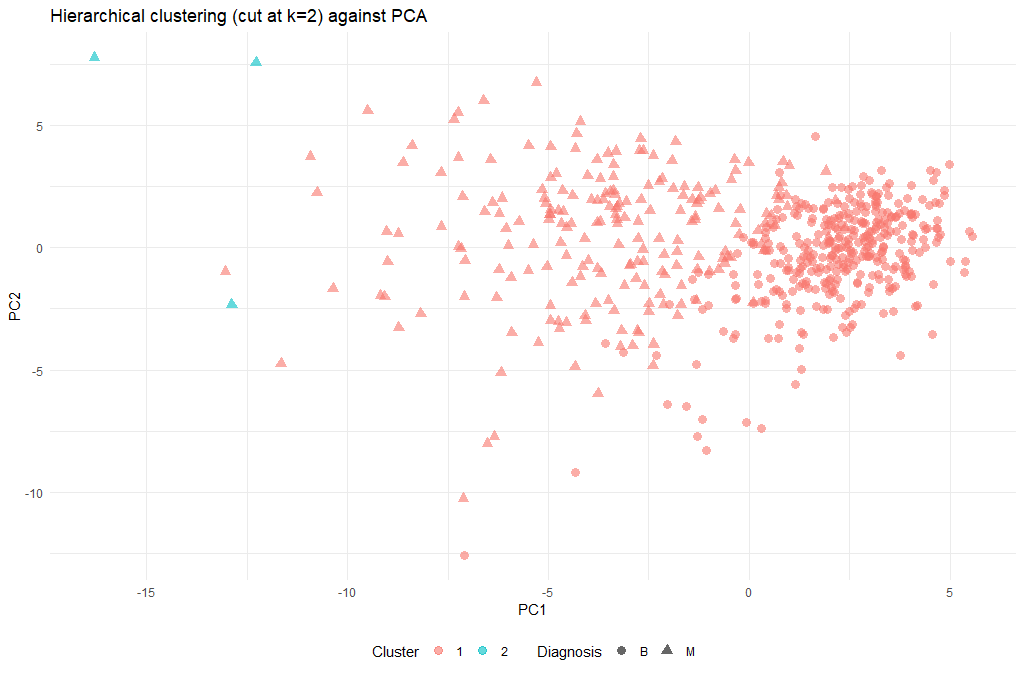
Next, we can cut the dendrogram in order to create the desired number of clusters. In our case, we might want to check whether our two groups (M and B) can be identified as sub-trees of our clustering - so we’ll set k = 2 and then plot the result.
cut_avg <- cutree(hclust_avg, k = 2)
plot(hclust_avg, labels = breastCancerData$ID, hang = -1, cex = 0.2,
main = "Cluster dendrogram (k = 2)", xlab = "Breast Cancer ID", ylab = "Height")
# k: Cut the dendrogram such that exactly k clusters are produced
# border: Vector with border colors for the rectangles. Coild also be a number vector 1:2
# which: A vector selecting the clusters around which a rectangle should be drawn (numbered from left to right)
rect.hclust(hclust_avg , k = 2, border = c("red","green"), which = c(1, 2))
# Draw a line at the height that the cut takes place
abline(h = 18, col = 'red', lwd=3, lty=2)
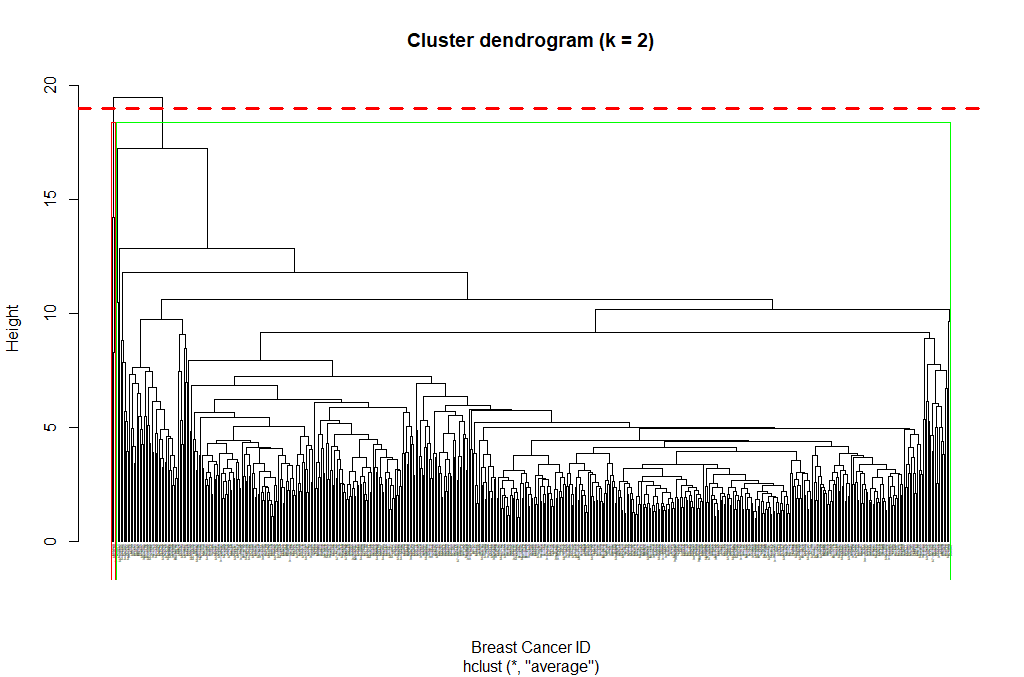
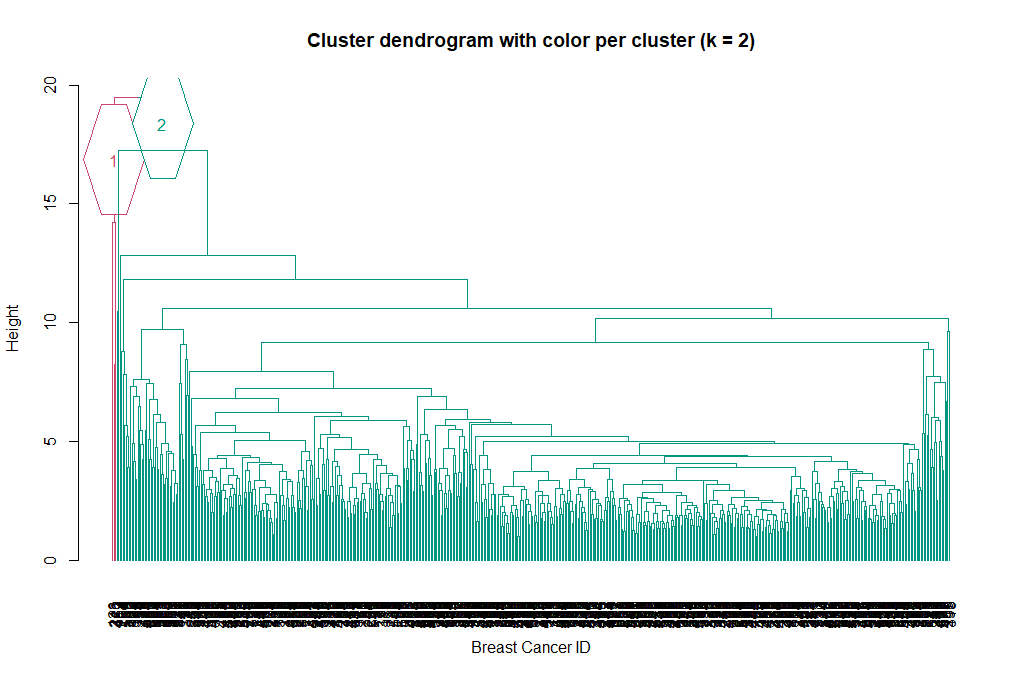
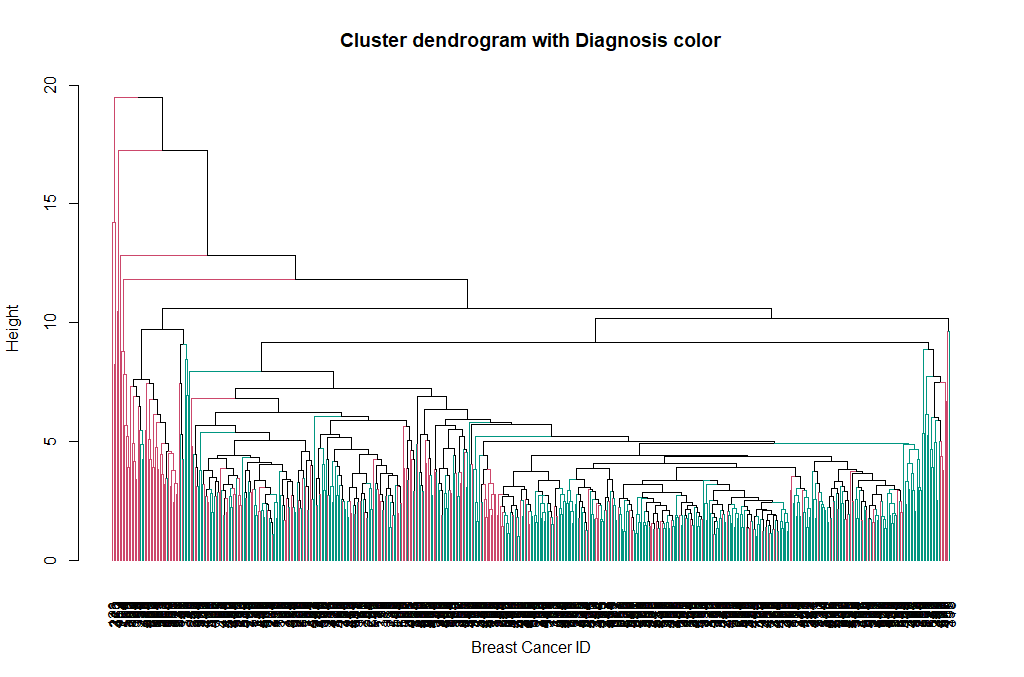
Now we can see the two clusters enclosed in two different colored boxes. We can also use the color_branches() function from the dendextend library to visualize our tree with different colored branches.
library(dendextend)
avg_dend_obj <- as.dendrogram(hclust_avg)
# We can use either k (number of clusters), or clusters (and specify the cluster type)
avg_col_dend <- color_branches(avg_dend_obj, k = 2, groupLabels=TRUE)
plot(avg_col_dend, main = "Cluster dendrogram with color per cluster (k = 2)", xlab = "Breast Cancer ID", ylab = "Height")
We can change the way branches are colored, to reflect the Diagnosis value:
avg_col_dend <- color_branches(avg_dend_obj, clusters = breastCancerData$Diagnosis)
plot(avg_col_dend, main = "Cluster dendrogram with Diagnosis color", xlab = "Breast Cancer ID", ylab = "Height")
ggplot(as.data.frame(ppv_pca$x), aes(x=PC1, y=PC2, color=as.factor(cut_avg), shape = breastCancerData$Diagnosis)) +
geom_point( alpha = 0.6, size = 3) +
theme_minimal()+
theme(legend.position = "bottom") +
labs(title = "Hierarchical clustering (cut at k=2) against PCA", x = "PC1", y = "PC2", color = "Cluster", shape = "Diagnosis")
| Exercises | |
|---|---|
| 1 | The hierarchical clustering performed so far, only used two methods: euclidean and average. Try experimenting with different methods. Do the final results improve? |
| 2 | Obviously the cut-off selection (k=2) was not optimal. Try using different cut-offs to ensure that the final clustering could provide some context to the original question. |